Space and Time Complexity Lesson
Observing the time complexity of different algorithms
- Space and Time Complexity
- Constant O(1)
- Linear O(n)
- Quadratic O(n^2)
- Logarithmic O(logn)
- Exponential O(2^n)
- Lesson notes
- Hacks
Space and Time Complexity
Space complexity refers to the amount of memory used by an algorithm to complete its execution, as a function of the size of the input. The space complexity of an algorithm can be affected by various factors such as the size of the input data, the data structures used in the algorithm, the number and size of temporary variables, and the recursion depth. Time complexity refers to the amount of time required by an algorithm to run as the input size grows. It is usually measured in terms of the "Big O" notation, which describes the upper bound of an algorithm's time complexity.
Why do you think a programmer should care about space and time complexity?
- A programmer should care about space and time complexity because a programmer can aim to have the most efficient running program for the intended program. Maybe a more complicated system with high powered computers and storage would be able to have a more complicated program that requires more time and space.
Take a look at our lassen volcano example from the data compression tech talk. The first code block is the original image. In the second code block, change the baseWidth to rescale the image.
from IPython.display import Image, display
from pathlib import Path
# prepares a series of images
def image_data(path=Path("images/"), images=None): # path of static images is defaulted
for image in images:
# File to open
image['filename'] = path / image['file'] # file with path
return images
def image_display(images):
for image in images:
display(Image(filename=image['filename']))
if __name__ == "__main__":
lassen_volcano = image_data(images=[{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
image_display(lassen_volcano)
from IPython.display import HTML, display
from pathlib import Path
from PIL import Image as pilImage
from io import BytesIO
import base64
# prepares a series of images
def image_data(path=Path("images/"), images=None): # path of static images is defaulted
for image in images:
# File to open
image['filename'] = path / image['file'] # file with path
return images
def scale_image(img):
#baseWidth = 625
#baseWidth = 1250
#baseWidth = 2500
baseWidth = 5000 # see the effect of doubling or halfing the baseWidth
#baseWidth = 10000
#baseWidth = 20000
#baseWidth = 40000
scalePercent = (baseWidth/float(img.size[0]))
scaleHeight = int((float(img.size[1])*float(scalePercent)))
scale = (baseWidth, scaleHeight)
return img.resize(scale)
def image_to_base64(img, format):
with BytesIO() as buffer:
img.save(buffer, format)
return base64.b64encode(buffer.getvalue()).decode()
def image_management(image): # path of static images is defaulted
# Image open return PIL image object
img = pilImage.open(image['filename'])
# Python Image Library operations
image['format'] = img.format
image['mode'] = img.mode
image['size'] = img.size
image['width'], image['height'] = img.size
image['pixels'] = image['width'] * image['height']
# Scale the Image
img = scale_image(img)
image['pil'] = img
image['scaled_size'] = img.size
image['scaled_width'], image['scaled_height'] = img.size
image['scaled_pixels'] = image['scaled_width'] * image['scaled_height']
# Scaled HTML
image['html'] = '<img src="data:image/png;base64,%s">' % image_to_base64(image['pil'], image['format'])
if __name__ == "__main__":
# Use numpy to concatenate two arrays
images = image_data(images = [{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
# Display meta data, scaled view, and grey scale for each image
for image in images:
image_management(image)
print("---- meta data -----")
print(image['label'])
print(image['source'])
print(image['format'])
print(image['mode'])
print("Original size: ", image['size'], " pixels: ", f"{image['pixels']:,}")
print("Scaled size: ", image['scaled_size'], " pixels: ", f"{image['scaled_pixels']:,}")
print("-- original image --")
display(HTML(image['html']))
Do you think this is a time complexity or space complexity or both problem?
- I think this is both a time complexity and space complexity problem because the larger the images, the more space they take up and the longer they take to load.
numbers = list(range(1000))
print(numbers)
print(numbers[263])
ncaa_bb_ranks = {1:"Alabama",2:"Houston", 3:"Purdue", 4:"Kansas"}
#look up a value in a dictionary given a key
print(ncaa_bb_ranks[1])
Space
This function takes two number inputs and returns their sum. The function does not create any additional data structures or variables that are dependent on the input size, so its space complexity is constant, or O(1). Regardless of how large the input numbers are, the function will always require the same amount of memory to execute.
def sum(a, b):
return a + b
print(sum(90,88))
print(sum(.9,.88))
Time
An example of a linear time algorithm is traversing a list or an array. When the size of the list or array increases, the time taken to traverse it also increases linearly with the size. Hence, the time complexity of this operation is O(n), where n is the size of the list or array being traversed.
for i in numbers:
print(i)
Space
This function takes a list of elements arr as input and returns a new list with the elements in reverse order. The function creates a new list reversed_arr of the same size as arr to store the reversed elements. The size of reversed_arr depends on the size of the input arr, so the space complexity of this function is O(n). As the input size increases, the amount of memory required to execute the function also increases linearly.
def reverse_list(arr):
n = len(arr)
reversed_arr = [None] * n #create a list of None based on the length or arr
for i in range(n):
reversed_arr[n-i-1] = arr[i] #stores the value at the index of arr to the value at the index of reversed_arr starting at the beginning for arr and end for reversed_arr
return reversed_arr
print(numbers)
print(reverse_list(numbers))
Time
An example of a quadratic time algorithm is nested loops. When there are two nested loops that both iterate over the same collection, the time taken to complete the algorithm grows quadratically with the size of the collection. Hence, the time complexity of this operation is O(n^2), where n is the size of the collection being iterated over.
for i in numbers:
for j in numbers:
print(i,j)
Space
This function takes two matrices matrix1 and matrix2 as input and returns their product as a new matrix. The function creates a new matrix result with dimensions m by n to store the product of the input matrices. The size of result depends on the size of the input matrices, so the space complexity of this function is O(n^2). As the size of the input matrices increases, the amount of memory required to execute the function also increases quadratically.
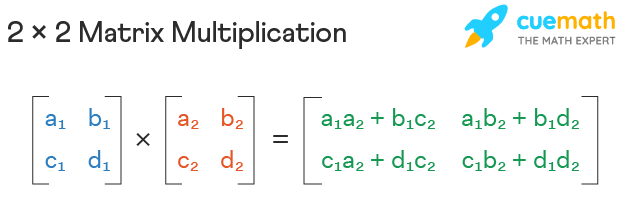
- Main take away is that a new matrix is created.
def multiply_matrices(matrix1, matrix2):
m = len(matrix1)
n = len(matrix2[0])
result = [[0] * n] * m #this creates the new matrix based on the size of matrix 1 and 2
for i in range(m):
for j in range(n):
for k in range(len(matrix2)):
result[i][j] += matrix1[i][k] * matrix2[k][j]
return result
print(multiply_matrices([[1,2],[3,4]], [[3,4],[1,2]]))
Time
An example of a log time algorithm is binary search. Binary search is an algorithm that searches for a specific element in a sorted list by repeatedly dividing the search interval in half. As a result, the time taken to complete the search grows logarithmically with the size of the list. Hence, the time complexity of this operation is O(log n), where n is the size of the list being searched.
def binary_search(arr, low, high, target):
while low <= high:
mid = (low + high) // 2 #integer division
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
target = 263
result = binary_search(numbers, 0, len(numbers) - 1, target)
print(result)
Space
The same algorithm above has a O(logn) space complexity. The function takes an array arr, its lower and upper bounds low and high, and a target value target. The function searches for target within the bounds of arr by recursively dividing the search space in half until the target is found or the search space is empty. The function does not create any new data structures that depend on the size of arr. Instead, the function uses the call stack to keep track of the recursive calls. Since the maximum depth of the recursive calls is O(logn), where n is the size of arr, the space complexity of this function is O(logn). As the size of arr increases, the amount of memory required to execute the function grows logarithmically.
Time
An example of an O(2^n) algorithm is the recursive implementation of the Fibonacci sequence. The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. The recursive implementation of the Fibonacci sequence calculates each number by recursively calling itself with the two preceding numbers until it reaches the base case (i.e., the first or second number in the sequence). The algorithm takes O(2^n) time in the worst case because it has to calculate each number in the sequence by making two recursive calls.
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
#print(fibonacci(5))
#print(fibonacci(10))
print(fibonacci(20))
#print(fibonacci(34))
#print(fibonacci(40))
Space
This function takes a set s as input and generates all possible subsets of s. The function does this by recursively generating the subsets of the set without the first element, and then adding the first element to each of those subsets to generate the subsets that include the first element. The function creates a new list for each recursive call that stores the subsets, and each element in the list is a new list that represents a subset. The number of subsets that can be generated from a set of size n is 2^n, so the space complexity of this function is O(2^n). As the size of the input set increases, the amount of memory required to execute the function grows exponentially.
def generate_subsets(s):
if not s:
return [[]]
subsets = generate_subsets(s[1:])
return [[s[0]] + subset for subset in subsets] + subsets
print(generate_subsets([1,2,3]))
print(generate_subsets([1,2,3,4,5,6]))
#print(generate_subsets(numbers))
Using the time library, we are able to see the difference in time it takes to calculate the fibonacci function above.
- Based on what is known about the other time complexities, hypothesize the resulting elapsed time if the function is replaced.
import time
start_time = time.time()
print(fibonacci(34))
end_time = time.time()
total_time = end_time - start_time
print("Time taken:", total_time, "seconds")
start_time = time.time()
print(fibonacci(36))
end_time = time.time()
total_time = end_time - start_time
print("Time taken:", total_time, "seconds")
Lesson notes
Big O complexity -> deals with space and time O(n) <- this is a linear progression specific value in list or dictionary = instant O(1) <- indexing directly Liner O(n) goes through a loop quadratic: O(n^2) has a nested loop so it takes a while < prints 1000x1000, counting at same time over and over again logarithmic O(logn): binary search algorithm permuting (permutations) = size, time, and complexity grows a lot
Hacks
-
Record your findings when testing the time elapsed of the different algorithms.
- linear O(n) = efficient algorithms (goes through loop)
- quadratic O(n^2) or O(2^n) = very inefficient algorithms (has a nested loop and prints 1000x1000), very slow
- logarithmic O(log(n)) = very efficient algorithms (binary search algorithm)= divides in half every time= decreases logarithmically
- O(2^n) ex. algorithm= recursive implementation of the Fibonacci sequence= makes two recursive calls = takes time and starts over
-
Although we will go more in depth later, time complexity is a key concept that relates to the different sorting algorithms. Do some basic research on the different types of sorting algorithms and their time complexity.
- Graph of the different algorithms and their time complexitites:
- website for sorting algorithms and time complexities
- selection sort= simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list
- bubble sort= simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order (not efficient)
- heap sort= comparison-based sorting technique based on Binary Heap data structure (similar to the selection sort where we first find the minimum element and place the minimum element at the beginning,repeat the same process for remaining elements)
- Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part
- here are some visual representations of these algorithims:
- Graph of the different algorithms and their time complexitites:
-
Why is time and space complexity important when choosing an algorithm?
- Time and space complexity are important when choosing an algorithm because a programmer wants to use the algorithm that is most efficient and takes the least space for their intended function. If the environment of the program has a lot more storage and device power, then a programmer can look into using an algorithm that uses more space and takes longer to run.
-
Should you always use a constant time algorithm / Should you never use an exponential time algorithm? Explain?
- These different algorithms are useful in different situations. For example, when computing a binary search, a constant time algorithm would take WAY too long for it would have to loop through every integer, so you should use an exponential time algorithm that would cut the list down in half every time. Although, when indexing a list, you would want to use a constant time algorithm because it can easily and efficiently find the value you are looking for.
-
What are some general patterns that you noticed to determine each algorithm's time and space complexity?
- I noticed that the more loops and nested loops an algorithm has, the slower it is. When there is an additional loops, the algorithm is increased by another power. For example, with the quadratic time algorithm, it has a nested loop. This causes it to have to run through the loops 1000 times (size of "numbers"), printing 1000 x 1000. This is very inefficient compared to the single loop of the linear time algorithm.
Complete the Time and Space Complexity analysis questions linked below. Practice
a = 0
b = 0
for i in range(N):
a = a + random()
for i in range(M):
b= b + random()
# Answer: O(N + M) time, O(1) space
a = 0;
for i in range(N):
for j in reversed(range(i,N)):
a = a + i + j;
# answer= 4: O(N*N)
k = 0;
for i in range(n//2,n):
for j in range(2,n,pow(2,j)):
k = k + n / 2;
# Answer: O(N log N)
- What does it mean when we say that an algorithm X is asymptotically more efficient than Y?
Answer= 2: X will always be a better choice for large inputs
a = 0
i = N
while (i > 0):
a += i
i //= 2
#Answer: O(log N)
- Which of the following best describes the useful criterion for comparing the efficiency of algorithms?
Time Memory Both of the above None of the above
Answer= 3: Both of the above
- How is time complexity measured?
By counting the number of algorithms in an algorithm. By counting the number of primitive operations performed by the algorithm on a given input size. By counting the size of data input to the algorithm. None of the above
Answer= By counting the number of primitive operations performed by the algorithm on a given input size.
for i in range(n):
i=i*k
# answer= 3. O(logkn)
value = 0;
for i in range(n):
for j in range(i):
value=value+1
# Answer: (n-1)
- Algorithm A and B have a worst-case running time of O(n) and O(logn), respectively. Therefore, algorithm B always runs faster than algorithm A.
True False
Answer= False